In this notebook, we will try to compute the stiffness matrix of a rectangular element using symbolic computations in Julia. Traditionally in undergraduate curriculum, computations of stiffness matrix for different elements are taught using hand calculations. However, using symbolic calculations along with matrix notation it is straight forward to derive those matrices. Though MATLAB is still widely used in engineering courses and also contains symbolic computation module, we will use Julia as it is open source and Julia’s matrix notations are nearly identical to that of MATLAB’s. Steps to run this notebook in VS Code along with different required installations can be found here .
Below, we will go over the steps followed to derive the element stiffness matrix. We will briefly go over the theory and use only the required equations. For a detailed exploration, readers are directed to the books mentioned in the references. Our example is focused on rectangular element only. However, the same approach can be followed for other elements with minor modifications.
Steps to derive element stiffness matrix:
Select the element type
Select displacement function
Define the strain-displacement and stress-strain relationships
Derive the element stiffness matrix
All the steps are briefly elaborated below along with the code to implement it. The notebook can be run from beginning to end sequentially to get the required results.
Note : This blog contains several equations. If equations are not rendered properly in this page, readers are requested to download the jupyter notebook (from above) and use it. All the content of this blog is also available in the jupyter notebook.
1. Select the element type
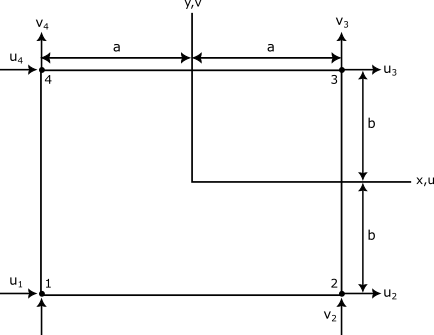
Bilinear Rectangle (Q4) Element
Bilinear Rectangle (Q4)
If the above figure is not clearly visible, consider changing the theme of background to “light”. Then the figure would be seen clearly. The element has 4 nodes and 8 degrees of freedom. It’s also called Q4 because it is a quadrilateral having 4 nodes. Standard counter-clockwise convention is used to name the nodes.
First load the relevant libraries. If a library is not installed, follow the instructions given in this link to download those.
using Symbolics , SymbolicNumericIntegration
ENV [ "COLUMNS" ] = 240 ; # For better display of symbolic columns
The variables to be used in the symbolic computation are defined below.
@variables x y a b ν ; # Last symbol "nu" can be obtained in Julia by "\nu" command.
2. Select the displacement function
In FEA, usually we are interested in the values of certain field quantities (for e.g., displacement) at the nodes and between the nodes. Therefore, interpolation is used to devise a continuous function that satisfies prescribed conditions (for e.g., for a compatible displacement field, element displacement must be linear along the edge between two nodes) at the nodes. For the rectangular element, following displacement function is used
$$u = a_1 + a_2x + a_3y + a_4 xy$$
$$v = a_5 + a_6x + a_7y + a_8 xy$$
Where, $a_1, a_2, \ldots, a_8$ are called generalized degrees of freedom. In matrix form, it can be written as
$$\begin{bmatrix}
u \\
v
\end{bmatrix} =
\begin{bmatrix}
1 & x & y & xy & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & x & y & xy
\end{bmatrix}
\begin{bmatrix}
a_1 \\
a_2 \\
a_3 \\
a_4 \\
a_5 \\
a_6 \\
a_7 \\
a_8
\end{bmatrix} = [X]_{2 \times 8} [a]_{8 \times 1}$$
In terms of nodal displacements, the displacement functions can be written as
\begin{equation}
\begin{bmatrix}
\phi_1 \\
\phi_2 \\
\phi_3 \\
\phi_4 \\
\phi_5 \\
\phi_6 \\
\phi_7 \\
\phi_8
\end{bmatrix} =
\begin{bmatrix}
1 & -a & -b & ab & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & -a & -b & ab \\
1 & a & -a & -ab & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & a & -b & -ab \\
1 & a & b & ab & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & a & b & ab \\
1 & -a & b & -ab & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & -a & b & -ab \\
\end{bmatrix}
\begin{bmatrix}
a_1 \\
a_2 \\
a_3 \\
a_4 \\
a_5 \\
a_6 \\
a_7 \\
a_8
\end{bmatrix} = [A]_{8 \times 8} [a]_{8 \times 1}
\end{equation}
Where displacements $\phi_1$, $\phi_2$, etc. are displacements at node 1, 2, etc. respectively. By substituting generalized coordinates obtained from nodal equations in displacement function, we get shape functions (or basis functions).
$$\begin{bmatrix}
u \\
v
\end{bmatrix} = [X]_{2 \times 8}
\begin{bmatrix}
a_1 \\
a_2 \\
a_3 \\
a_4 \\
a_5 \\
a_6 \\
a_7 \\
a_8
\end{bmatrix} = [X]_{2 \times 8} [A^{-1}]_{8 \times 8}
\begin{bmatrix}
\phi_1 \\
\phi_2 \\
\phi_3 \\
\phi_4 \\
\phi_5 \\
\phi_6 \\
\phi_7 \\
\phi_8
\end{bmatrix} = [N]_{2 \times 8}
\begin{bmatrix}
\phi_1 \\
\phi_2 \\
\phi_3 \\
\phi_4 \\
\phi_5 \\
\phi_6 \\
\phi_7 \\
\phi_8
\end{bmatrix}
$$
By running following code cells, we can obtain the expression for shape function matrix.
X = [ 1 x y x * y 0 0 0 0 ; 0 0 0 0 1 x y x * y ]
$$ \begin{equation}
\left[
\begin{array}{cccccccc}
1 & x & y & x y & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & x & y & x y \\
\end{array}
\right]
\end{equation}
$$
A = [ 1 - a - b a * b 0 0 0 0 ;
0 0 0 0 1 - a - b a * b ;
1 a - b - a * b 0 0 0 0 ;
0 0 0 0 1 a - b - a * b ;
1 a b a * b 0 0 0 0 ;
0 0 0 0 1 a b a * b ;
1 - a b - a * b 0 0 0 0 ;
0 0 0 0 1 - a b - a * b ]
$$ \begin{equation}
\left[
\begin{array}{cccccccc}
1 & - a & - b & a b & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & - a & - b & a b \\
1 & a & - b & - a b & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & a & - b & - a b \\
1 & a & b & a b & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & a & b & a b \\
1 & - a & b & - a b & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & - a & b & - a b \\
\end{array}
\right]
\end{equation}
$$
\begin{equation}
\left[
\begin{array}{cccccccc}
\frac{1}{4} + \frac{ - y}{4 b} + \frac{x y}{4 a b} + \frac{ - x}{4 a} & 0 & \frac{1}{4} + \frac{ - x y}{4 a b} + \frac{ - y}{4 b} + \frac{x}{4 a} & 0 & \frac{1}{4} + \frac{y}{4 b} + \frac{x y}{4 a b} + \frac{x}{4 a} & 0 & \frac{1}{4} + \frac{ - x y}{4 a b} + \frac{y}{4 b} + \frac{ - x}{4 a} & 0 \\
0 & \frac{1}{4} + \frac{ - y}{4 b} + \frac{x y}{4 a b} + \frac{ - x}{4 a} & 0 & \frac{1}{4} + \frac{ - x y}{4 a b} + \frac{ - y}{4 b} + \frac{x}{4 a} & 0 & \frac{1}{4} + \frac{y}{4 b} + \frac{x y}{4 a b} + \frac{x}{4 a} & 0 & \frac{1}{4} + \frac{ - x y}{4 a b} + \frac{y}{4 b} + \frac{ - x}{4 a} \\
\end{array}
\right]
\end{equation}
3. Define strain-displacement and stress-strain relationship
Using the definition of axial and shear strain, the strain-displacement equation (in matrix form) can be written as follows:
$$\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix} =
\begin{bmatrix}
\frac{\partial}{\partial x} & 0 \\
0 & \frac{\partial}{\partial y} \\
\frac{\partial}{\partial y} & \frac{\partial}{\partial x}
\end{bmatrix}
\begin{bmatrix}
u \\
v
\end{bmatrix}
$$
In terms of nodal coordinates, the above equation can also be written as:
$$
\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix} =
\begin{bmatrix}
\frac{\partial}{\partial x} & 0 \\
0 & \frac{\partial}{\partial y} \\
\frac{\partial}{\partial y} & \frac{\partial}{\partial x}
\end{bmatrix}
[N]_{2 \times 8}
\begin{bmatrix}
\phi_1 \\
\phi_2 \\
\phi_3 \\
\phi_4 \\
\phi_5 \\
\phi_6 \\
\phi_7 \\
\phi_8
\end{bmatrix} =
[B]_{3 \times 8}
\begin{bmatrix}
\phi_1 \\
\phi_2 \\
\phi_3 \\
\phi_4 \\
\phi_5 \\
\phi_6 \\
\phi_7 \\
\phi_8
\end{bmatrix}
$$
We need the [B] matrix as that would be used in the computation of stiffness matrix. In the cell below we define the differential operators with respect to x and y.
D_x = Differential ( x )
D_y = Differential ( y )
(::Differential) (generic function with 3 methods)
Then we apply the operator to the first row of [N] matrix.
[ expand_derivatives ( D_x ( item )) for item in N [ 1 , : ]]
$$ \begin{equation}
\left[
\begin{array}{c}
\frac{-1}{4 a} + \frac{y}{4 a b} \\
0 \\
\frac{1}{4 a} + \frac{ - y}{4 a b} \\
0 \\
\frac{y}{4 a b} + \frac{1}{4 a} \\
0 \\
\frac{-1}{4 a} + \frac{ - y}{4 a b} \\
0 \\
\end{array}
\right]
\end{equation}
$$
B = vcat ([ expand_derivatives ( D_x ( item )) for item in N [ 1 , : ]] ' ,
[ expand_derivatives ( D_y ( item )) for item in N [ 2 , : ]] ' ,
[ expand_derivatives ( D_y ( item )) for item in N [ 1 , : ]] ' + [ expand_derivatives ( D_x ( item )) for item in N [ 2 , : ]] ' )
\begin{equation}
\left[
\begin{array}{cccccccc}
\frac{-1}{4 a} + \frac{y}{4 a b} & 0 & \frac{1}{4 a} + \frac{ - y}{4 a b} & 0 & \frac{y}{4 a b} + \frac{1}{4 a} & 0 & \frac{-1}{4 a} + \frac{ - y}{4 a b} & 0 \\
0 & \frac{x}{4 a b} + \frac{-1}{4 b} & 0 & \frac{ - x}{4 a b} + \frac{-1}{4 b} & 0 & \frac{x}{4 a b} + \frac{1}{4 b} & 0 & \frac{ - x}{4 a b} + \frac{1}{4 b} \\
\frac{x}{4 a b} + \frac{-1}{4 b} & \frac{-1}{4 a} + \frac{y}{4 a b} & \frac{ - x}{4 a b} + \frac{-1}{4 b} & \frac{1}{4 a} + \frac{ - y}{4 a b} & \frac{x}{4 a b} + \frac{1}{4 b} & \frac{y}{4 a b} + \frac{1}{4 a} & \frac{ - x}{4 a b} + \frac{1}{4 b} & \frac{-1}{4 a} + \frac{ - y}{4 a b} \\
\end{array}
\right]
\end{equation}
4. Derive the element stiffness matrix
Without derivation, we define the stiffness matrix as:
$$[k]_{8 \times 8} = \int_{-b}^b \int_{-a}^{a}[B]^T_{8 \times 3}[E]_{3 \times 3} [B]_{3 \times 8} t dx dy$$
Where $t$ is the element thickness. Matrix $[E]$ is called the constitutive matrix (it is also named as [D] in some literature).For a derivation, readers are directed to the the excellent books in the references. In the following cell, we define $[E] * (1 - \nu^2)$. We do so to remove $(1 - \nu^2)$ term from all the entries of stiffness matrix.
# Consider the [E] (constitutive matrix) below as product of E (elastic modulus) and (1 - ν^2)
E = [ 1 ν 0 ;
ν 1 0
0 0 ( 1 - ν ) / 2 ]
$$ \begin{equation}
\left[
\begin{array}{ccc}
1 & \nu & 0 \\
\nu & 1 & 0 \\
0 & 0 & \frac{1}{2} \left( 1 - \nu \right) \\
\end{array}
\right]
\end{equation}
$$
\begin{equation}
\left[
\begin{array}{cccccccc}
\left( \frac{-1}{4 a} + \frac{y}{4 a b} \right)^{2} + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right)^{2} \left( 1 - \nu \right) & \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \nu + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \nu + \frac{1}{2} \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) \\
\left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \nu + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right)^{2} + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right)^{2} \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( 1 - \nu \right) + \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) + \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \nu & \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( 1 - \nu \right) + \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \nu & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( 1 - \nu \right) \\
\left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( 1 - \nu \right) + \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu & \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right)^{2} + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right)^{2} \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) + \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu & \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) + \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu \\
\left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right)^{2} + \frac{1}{2} \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right)^{2} \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \nu + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) \\
\left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) + \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \nu & \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \nu + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{y}{4 a b} + \frac{1}{4 a} \right)^{2} + \frac{1}{2} \left( \frac{x}{4 a b} + \frac{1}{4 b} \right)^{2} \left( 1 - \nu \right) & \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \nu + \frac{1}{2} \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \nu + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) \\
\left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \nu + \frac{1}{2} \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) + \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \nu + \frac{1}{2} \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{x}{4 a b} + \frac{1}{4 b} \right)^{2} + \frac{1}{2} \left( \frac{y}{4 a b} + \frac{1}{4 a} \right)^{2} \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) + \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \nu & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) \\
\left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( 1 - \nu \right) + \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \nu & \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) + \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \nu & \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right)^{2} + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right)^{2} \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) \\
\left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{-1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{-1}{4 a} + \frac{y}{4 a b} \right) \left( 1 - \nu \right) & \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) + \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \nu & \left( \frac{ - x}{4 a b} + \frac{-1}{4 b} \right) \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \nu + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{x}{4 a b} + \frac{1}{4 b} \right) + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( \frac{y}{4 a b} + \frac{1}{4 a} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \nu + \frac{1}{2} \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right) \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right) \left( 1 - \nu \right) & \left( \frac{ - x}{4 a b} + \frac{1}{4 b} \right)^{2} + \frac{1}{2} \left( \frac{-1}{4 a} + \frac{ - y}{4 a b} \right)^{2} \left( 1 - \nu \right) \\
\end{array}
\right]
\end{equation}
Substituting values in place of a (width) and b (height). We do so to reduce the number of symbolic variables and simplify expressions further.
K_evaluated = substitute ( K , Dict ( a => 0.5 , b => 0.5 ))
\begin{equation}
\left[
\begin{array}{cccccccc}
\left( -0.5 + y \right)^{2} + \frac{1}{2} \left( -0.5 + x \right)^{2} \left( 1 - \nu \right) & \left( -0.5 + x \right) \left( -0.5 + y \right) \nu + \frac{1}{2} \left( -0.5 + x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) & \left( -0.5 + y \right) \left( 0.5 - y \right) + \frac{1}{2} \left( -0.5 - x \right) \left( -0.5 + x \right) \left( 1 - \nu \right) & \frac{1}{2} \left( -0.5 + x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) + \left( -0.5 - x \right) \left( -0.5 + y \right) \nu & \left( -0.5 + y \right) \left( 0.5 + y \right) + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 + x \right) \left( 1 - \nu \right) & \frac{1}{2} \left( -0.5 + x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) + \left( 0.5 + x \right) \left( -0.5 + y \right) \nu & \left( -0.5 - y \right) \left( -0.5 + y \right) + \frac{1}{2} \left( -0.5 + x \right) \left( 0.5 - x \right) \left( 1 - \nu \right) & \frac{1}{2} \left( -0.5 + x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) + \left( 0.5 - x \right) \left( -0.5 + y \right) \nu \\
\left( -0.5 + x \right) \left( -0.5 + y \right) \nu + \frac{1}{2} \left( -0.5 + x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) & \left( -0.5 + x \right)^{2} + \frac{1}{2} \left( -0.5 + y \right)^{2} \left( 1 - \nu \right) & \left( -0.5 + x \right) \left( 0.5 - y \right) \nu + \frac{1}{2} \left( -0.5 - x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) & \left( -0.5 - x \right) \left( -0.5 + x \right) + \frac{1}{2} \left( -0.5 + y \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( -0.5 + x \right) \left( 0.5 + y \right) \nu + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( -0.5 + x \right) + \frac{1}{2} \left( -0.5 + y \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \frac{1}{2} \left( 0.5 - x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) + \left( -0.5 + x \right) \left( -0.5 - y \right) \nu & \left( -0.5 + x \right) \left( 0.5 - x \right) + \frac{1}{2} \left( -0.5 - y \right) \left( -0.5 + y \right) \left( 1 - \nu \right) \\
\left( -0.5 + y \right) \left( 0.5 - y \right) + \frac{1}{2} \left( -0.5 - x \right) \left( -0.5 + x \right) \left( 1 - \nu \right) & \left( -0.5 + x \right) \left( 0.5 - y \right) \nu + \frac{1}{2} \left( -0.5 - x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) & \left( 0.5 - y \right)^{2} + \frac{1}{2} \left( -0.5 - x \right)^{2} \left( 1 - \nu \right) & \left( -0.5 - x \right) \left( 0.5 - y \right) \nu + \frac{1}{2} \left( -0.5 - x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( 0.5 + y \right) \left( 0.5 - y \right) + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 - x \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( 0.5 - y \right) \nu + \frac{1}{2} \left( -0.5 - x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \left( -0.5 - y \right) \left( 0.5 - y \right) + \frac{1}{2} \left( -0.5 - x \right) \left( 0.5 - x \right) \left( 1 - \nu \right) & \frac{1}{2} \left( -0.5 - x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) + \left( 0.5 - x \right) \left( 0.5 - y \right) \nu \\
\frac{1}{2} \left( -0.5 + x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) + \left( -0.5 - x \right) \left( -0.5 + y \right) \nu & \left( -0.5 - x \right) \left( -0.5 + x \right) + \frac{1}{2} \left( -0.5 + y \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( -0.5 - x \right) \left( 0.5 - y \right) \nu + \frac{1}{2} \left( -0.5 - x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( -0.5 - x \right)^{2} + \frac{1}{2} \left( 0.5 - y \right)^{2} \left( 1 - \nu \right) & \frac{1}{2} \left( 0.5 + x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) + \left( -0.5 - x \right) \left( 0.5 + y \right) \nu & \left( 0.5 + x \right) \left( -0.5 - x \right) + \frac{1}{2} \left( 0.5 + y \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( -0.5 - x \right) \left( -0.5 - y \right) \nu + \frac{1}{2} \left( 0.5 - x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( -0.5 - x \right) \left( 0.5 - x \right) + \frac{1}{2} \left( -0.5 - y \right) \left( 0.5 - y \right) \left( 1 - \nu \right) \\
\left( -0.5 + y \right) \left( 0.5 + y \right) + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 + x \right) \left( 1 - \nu \right) & \left( -0.5 + x \right) \left( 0.5 + y \right) \nu + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) & \left( 0.5 + y \right) \left( 0.5 - y \right) + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 - x \right) \left( 1 - \nu \right) & \frac{1}{2} \left( 0.5 + x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) + \left( -0.5 - x \right) \left( 0.5 + y \right) \nu & \left( 0.5 + y \right)^{2} + \frac{1}{2} \left( 0.5 + x \right)^{2} \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( 0.5 + y \right) \nu + \frac{1}{2} \left( 0.5 + x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \left( -0.5 - y \right) \left( 0.5 + y \right) + \frac{1}{2} \left( 0.5 + x \right) \left( 0.5 - x \right) \left( 1 - \nu \right) & \left( 0.5 - x \right) \left( 0.5 + y \right) \nu + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) \\
\frac{1}{2} \left( -0.5 + x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) + \left( 0.5 + x \right) \left( -0.5 + y \right) \nu & \left( 0.5 + x \right) \left( -0.5 + x \right) + \frac{1}{2} \left( -0.5 + y \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( 0.5 - y \right) \nu + \frac{1}{2} \left( -0.5 - x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( -0.5 - x \right) + \frac{1}{2} \left( 0.5 + y \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( 0.5 + y \right) \nu + \frac{1}{2} \left( 0.5 + x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \left( 0.5 + x \right)^{2} + \frac{1}{2} \left( 0.5 + y \right)^{2} \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( -0.5 - y \right) \nu + \frac{1}{2} \left( 0.5 - x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( 0.5 - x \right) + \frac{1}{2} \left( -0.5 - y \right) \left( 0.5 + y \right) \left( 1 - \nu \right) \\
\left( -0.5 - y \right) \left( -0.5 + y \right) + \frac{1}{2} \left( -0.5 + x \right) \left( 0.5 - x \right) \left( 1 - \nu \right) & \frac{1}{2} \left( 0.5 - x \right) \left( -0.5 + y \right) \left( 1 - \nu \right) + \left( -0.5 + x \right) \left( -0.5 - y \right) \nu & \left( -0.5 - y \right) \left( 0.5 - y \right) + \frac{1}{2} \left( -0.5 - x \right) \left( 0.5 - x \right) \left( 1 - \nu \right) & \left( -0.5 - x \right) \left( -0.5 - y \right) \nu + \frac{1}{2} \left( 0.5 - x \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( -0.5 - y \right) \left( 0.5 + y \right) + \frac{1}{2} \left( 0.5 + x \right) \left( 0.5 - x \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( -0.5 - y \right) \nu + \frac{1}{2} \left( 0.5 - x \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \left( -0.5 - y \right)^{2} + \frac{1}{2} \left( 0.5 - x \right)^{2} \left( 1 - \nu \right) & \frac{1}{2} \left( 0.5 - x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) + \left( 0.5 - x \right) \left( -0.5 - y \right) \nu \\
\frac{1}{2} \left( -0.5 + x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) + \left( 0.5 - x \right) \left( -0.5 + y \right) \nu & \left( -0.5 + x \right) \left( 0.5 - x \right) + \frac{1}{2} \left( -0.5 - y \right) \left( -0.5 + y \right) \left( 1 - \nu \right) & \frac{1}{2} \left( -0.5 - x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) + \left( 0.5 - x \right) \left( 0.5 - y \right) \nu & \left( -0.5 - x \right) \left( 0.5 - x \right) + \frac{1}{2} \left( -0.5 - y \right) \left( 0.5 - y \right) \left( 1 - \nu \right) & \left( 0.5 - x \right) \left( 0.5 + y \right) \nu + \frac{1}{2} \left( 0.5 + x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) & \left( 0.5 + x \right) \left( 0.5 - x \right) + \frac{1}{2} \left( -0.5 - y \right) \left( 0.5 + y \right) \left( 1 - \nu \right) & \frac{1}{2} \left( 0.5 - x \right) \left( -0.5 - y \right) \left( 1 - \nu \right) + \left( 0.5 - x \right) \left( -0.5 - y \right) \nu & \left( 0.5 - x \right)^{2} + \frac{1}{2} \left( -0.5 - y \right)^{2} \left( 1 - \nu \right) \\
\end{array}
\right]
\end{equation}
First, integrating with respect to x and applying limits.
first_integration_wrt_x_elementwise = map ( element -> integrate ( element , ( x , - 0.5 , 0.5 ); detailed = false , symbolic = true ), K_evaluated )
8×8 Matrix{SymbolicUtils.BasicSymbolic{Real}}:
0.416667 - y - 0.166667ν + y^2 0.125 - 0.25y + 0.125ν - 0.25y*ν -0.166667 + y - 0.0833333ν - (y^2) … 0.0833333 + 0.166667ν - (y^2) 0.125 + 0.25y - 0.375ν + 0.25y*ν
0.125 - 0.25y + 0.125ν - 0.25y*ν 0.458333 - 0.5y - 0.125ν + 0.5(y^2) + 0.5y*ν - 0.5(y^2)*ν 0.125 - 0.25y - 0.375ν + 0.75y*ν -0.125 + 0.25y + 0.375ν + 0.25y*ν -0.208333 - 0.125ν - 0.5(y^2) + 0.5(y^2)*ν
-0.166667 + y - 0.0833333ν - (y^2) 0.125 - 0.25y - 0.375ν + 0.75y*ν 0.416667 - y - 0.166667ν + y^2 -0.333333 + 0.0833333ν + y^2 0.125 + 0.25y + 0.125ν - 0.75y*ν
-0.125 + 0.25y + 0.375ν - 0.75y*ν 0.0416667 + 0.5y + 0.125ν - 0.5(y^2) - 0.5y*ν + 0.5(y^2)*ν -0.125 + 0.25y - 0.125ν + 0.25y*ν 0.125 - 0.25y + 0.125ν + 0.75y*ν -0.291667 + 0.125ν + 0.5(y^2) - 0.5(y^2)*ν
-0.333333 + 0.0833333ν + y^2 -0.125 + 0.25y - 0.125ν - 0.75y*ν 0.0833333 + 0.166667ν - (y^2) -0.166667 - y - 0.0833333ν - (y^2) -0.125 - 0.25y + 0.375ν + 0.75y*ν
-0.125 - 0.25y - 0.125ν + 0.75y*ν -0.291667 + 0.125ν + 0.5(y^2) - 0.5(y^2)*ν -0.125 - 0.25y + 0.375ν - 0.25y*ν … 0.125 + 0.25y - 0.375ν - 0.75y*ν 0.0416667 - 0.5y + 0.125ν - 0.5(y^2) + 0.5y*ν + 0.5(y^2)*ν
0.0833333 + 0.166667ν - (y^2) -0.125 + 0.25y + 0.375ν + 0.25y*ν -0.333333 + 0.0833333ν + y^2 0.416667 + y - 0.166667ν + y^2 -0.125 - 0.25y - 0.125ν - 0.25y*ν
0.125 + 0.25y - 0.375ν + 0.25y*ν -0.208333 - 0.125ν - 0.5(y^2) + 0.5(y^2)*ν 0.125 + 0.25y + 0.125ν - 0.75y*ν -0.125 - 0.25y - 0.125ν - 0.25y*ν 0.458333 + 0.5y - 0.125ν + 0.5(y^2) - 0.5y*ν - 0.5(y^2)*ν
Some matrix elements are not shown in the above matrix. We then integrate with respect to y and apply limits.
second_integration_wrt_y_elementwise = map ( element -> integrate ( element , ( y , - 0.5 , 0.5 ); detailed = false , symbolic = true ), first_integration_wrt_x_elementwise )
8×8 Matrix{SymbolicUtils.BasicSymbolic{Real}}:
0.5 - 0.166667ν 0.125 + 0.125ν -0.25 - 0.0833333ν -0.125 + 0.375ν -0.25 + 0.0833333ν -0.125 - 0.125ν 0.166667ν 0.125 - 0.375ν
0.125 + 0.125ν 0.5 - 0.166667ν 0.125 - 0.375ν 6.93889e-18 + 0.166667ν -0.125 - 0.125ν -0.25 + 0.0833333ν -0.125 + 0.375ν -0.25 - 0.0833333ν
-0.25 - 0.0833333ν 0.125 - 0.375ν 0.5 - 0.166667ν -0.125 - 0.125ν 0.166667ν -0.125 + 0.375ν -0.25 + 0.0833333ν 0.125 + 0.125ν
-0.125 + 0.375ν 6.93889e-18 + 0.166667ν -0.125 - 0.125ν 0.5 - 0.166667ν 0.125 - 0.375ν -0.25 - 0.0833333ν 0.125 + 0.125ν -0.25 + 0.0833333ν
-0.25 + 0.0833333ν -0.125 - 0.125ν 0.166667ν 0.125 - 0.375ν 0.5 - 0.166667ν 0.125 + 0.125ν -0.25 - 0.0833333ν -0.125 + 0.375ν
-0.125 - 0.125ν -0.25 + 0.0833333ν -0.125 + 0.375ν -0.25 - 0.0833333ν 0.125 + 0.125ν 0.5 - 0.166667ν 0.125 - 0.375ν 6.93889e-18 + 0.166667ν
0.166667ν -0.125 + 0.375ν -0.25 + 0.0833333ν 0.125 + 0.125ν -0.25 - 0.0833333ν 0.125 - 0.375ν 0.5 - 0.166667ν -0.125 - 0.125ν
0.125 - 0.375ν -0.25 - 0.0833333ν 0.125 + 0.125ν -0.25 + 0.0833333ν -0.125 + 0.375ν 6.93889e-18 + 0.166667ν -0.125 - 0.125ν 0.5 - 0.166667ν
For a check of the results, we can compare our obtained stiffness matrix with the stiffness matrix reported in reference 3 (code line number 87 to 99 in paper).
Caveat
Though the symbolic approach works well for the rectangular element, it might not work for more complex elements. This is because the symbolic integrations are not always exact. Symbolic integrations in Julia usually produce the solution along with an unsolved portion and error. Fortunately, in our case we did not require the error term. It is also a good practice to substitute values (of symbols) wherever possible to simplify the expression rather than doing all the computations symbolically and then substituting the values at the end.
References
Concepts and applications of finite element analysis by Robert D. Cook, et. al. (John Wiley & Sons, Inc., Fourth Edition)
A first course in the finite element method by Daryl L. Logan (Cengage Learning, Fifth Edition)
A 99 line topology optimization code written in MATLAB (Springer, 2001) by Ole Sigmund (Link: https://www.topopt.mek.dtu.dk/apps-and-software/a-99-line-topology-optimization-code-written-in-matlab , Last accessed: 25 Feb 2024)
 View source on GitHub
View source on GitHub